Area Between Curves Calculator: Find Integrals Fast

<!DOCTYPE html>
Calculating the area between curves is a fundamental concept in calculus, essential for solving problems in physics, engineering, and mathematics. Whether you’re a student or a professional, understanding how to find the area between two curves can save you time and effort. An area between curves calculator simplifies this process, allowing you to compute integrals quickly and accurately. This tool is particularly useful for complex functions where manual integration can be tedious and error-prone. By leveraging technology, you can focus on analyzing results rather than performing lengthy calculations. (area between curves calculator, integral calculator, calculus tools)
Why Use an Area Between Curves Calculator?
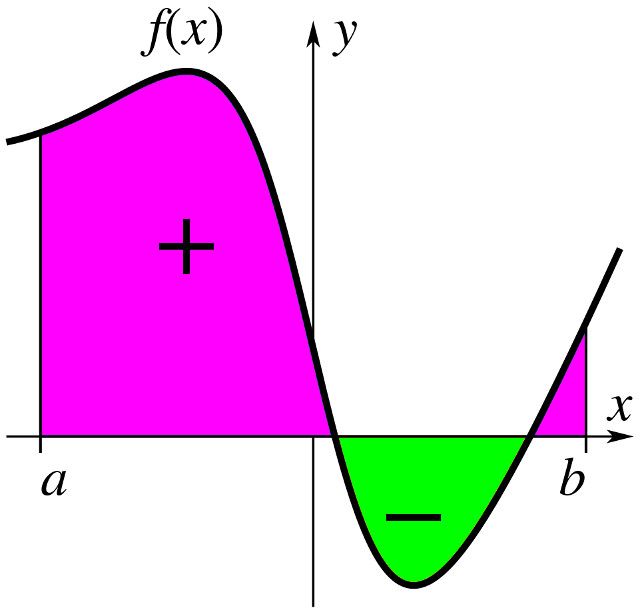
An area between curves calculator is a powerful tool that automates the process of finding the area between two functions over a given interval. It eliminates the need for manual integration, reducing the risk of errors and saving valuable time. This calculator is especially beneficial for:
- Students tackling calculus assignments
- Professionals working on real-world applications
- Researchers analyzing data with complex functions
By inputting the functions and the limits of integration, the calculator provides instant results, making it an indispensable resource for anyone dealing with integrals. (calculus calculator, area between functions, integration tool)
How to Use an Area Between Curves Calculator
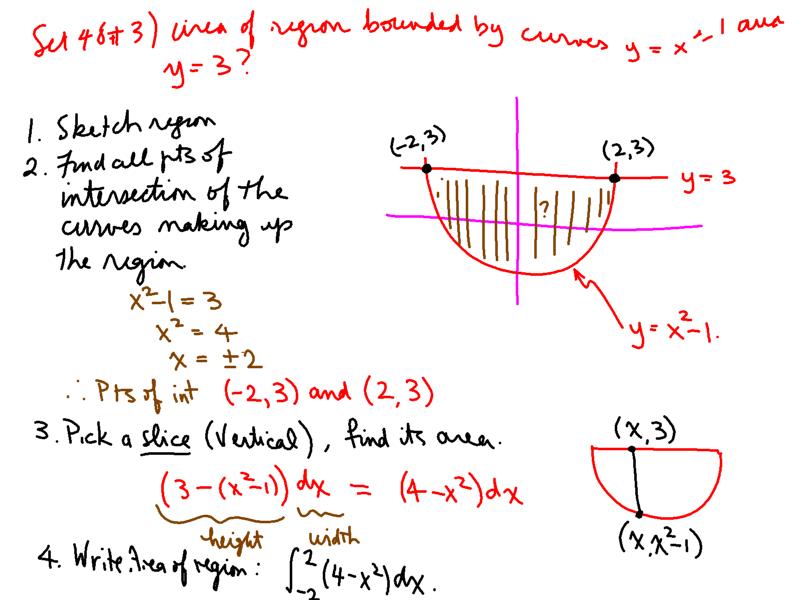
Using an area between curves calculator is straightforward. Follow these steps to find the area between two curves efficiently:
Step 1: Define the Functions
Identify the two functions, ( f(x) ) and ( g(x) ), between which you want to calculate the area. Ensure that ( f(x) \geq g(x) ) over the interval ([a, b]). (define functions, interval calculation)
Step 2: Input the Functions and Interval
Enter the functions and the interval ([a, b]) into the calculator. Most tools allow you to type the functions directly or select from predefined examples. (input functions, interval limits)
Step 3: Calculate the Area
Click the “Calculate” button to find the area between the curves. The calculator will compute the definite integral ( \int_{a}^{b} [f(x) - g(x)] \, dx ) and display the result. (calculate area, definite integral)
📌 Note: Always verify the functions and interval before calculating to ensure accurate results.
Benefits of Using an Area Between Curves Calculator

The area between curves calculator offers several advantages, including:
| Benefit | Description |
|---|---|
| Time-Saving | Automates complex calculations, reducing manual effort. |
| Accuracy | Minimizes errors associated with manual integration. |
| Versatility | Handles a wide range of functions and intervals. |
| User-Friendly | Simple interface suitable for beginners and experts alike. |
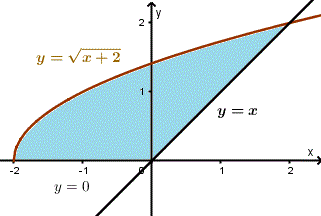
These benefits make the calculator an essential tool for anyone working with integrals. (time-saving calculator, accurate integration, versatile tool)
Checklist for Using an Area Between Curves Calculator

To ensure accurate results, follow this checklist when using an area between curves calculator:
- Verify the functions ( f(x) ) and ( g(x) ) are correctly defined.
- Confirm the interval ([a, b]) is appropriate for the problem.
- Check that ( f(x) \geq g(x) ) over the entire interval.
- Double-check the input before calculating.
- Review the result to ensure it makes sense in the context of the problem.
Following these steps will help you avoid common mistakes and obtain reliable results. (calculator checklist, accurate results, problem-solving tips)
What is an area between curves calculator?
+An area between curves calculator is a tool that computes the area between two functions over a specified interval using definite integrals.
How do I input functions into the calculator?
+Most calculators allow you to type the functions directly, such as ( f(x) = x^2 ) and ( g(x) = x ), or select from predefined examples.
Can the calculator handle complex functions?
+Yes, the calculator can handle a wide range of functions, including polynomials, trigonometric, and exponential functions.
In summary, an area between curves calculator is a valuable tool for anyone working with integrals. It simplifies the process of finding the area between two functions, saving time and reducing errors. By following the steps and checklist provided, you can ensure accurate results and make the most of this powerful calculator. Whether you’re a student or a professional, this tool is an essential addition to your mathematical toolkit. (integral calculator, calculus tool, mathematical solutions)


