Polar Curve Area Calculator: Quick & Easy Integration Tool

<!DOCTYPE html>
Calculating the area under a polar curve can be a complex task, but with the right tools, it becomes a breeze. Whether you're a student, researcher, or professional, a Polar Curve Area Calculator simplifies the process of integrating polar equations. This tool not only saves time but also ensures accuracy, making it an essential resource for anyone dealing with polar coordinates. In this post, we’ll explore how to use this calculator effectively, its benefits, and why it’s a must-have for mathematical tasks. (polar curve calculator, area under polar curve, integration tool)
What is a Polar Curve Area Calculator?

A Polar Curve Area Calculator is a specialized tool designed to compute the area enclosed by a polar curve. Unlike Cartesian coordinates, polar coordinates use radius and angle to define points, making area calculations more intricate. This calculator automates the integration process, providing quick and accurate results. It’s particularly useful for tasks involving calculus, geometry, and engineering. (polar coordinates, area calculation, mathematical tools)
How Does the Polar Curve Area Calculator Work?
The calculator uses the formula for the area under a polar curve: A = (1⁄2) ∫[a, b] r² dθ, where r is the polar equation and θ is the angle. Here’s a breakdown of the steps:
- Input the Polar Equation: Enter the equation of the polar curve.
- Set the Limits of Integration: Define the start and end angles (a and b).
- Calculate: The tool integrates the equation over the specified range and computes the area.
📘 Note: Ensure the equation is in terms of θ and the limits are in radians for accurate results.
Benefits of Using a Polar Curve Area Calculator

Here are some key advantages of using this tool:
- Time-Saving: Automates complex calculations, reducing manual effort.
- Accuracy: Minimizes errors common in manual integration.
- User-Friendly: Intuitive interface suitable for beginners and experts alike.
- Versatility: Handles a wide range of polar equations and applications.
When to Use a Polar Curve Area Calculator
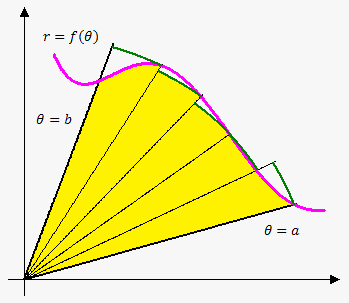
This tool is ideal for various scenarios, including:
- Solving calculus problems involving polar curves.
- Designing geometric shapes in engineering or architecture.
- Analyzing data in physics or astronomy.
- Teaching or learning advanced mathematical concepts.
Step-by-Step Guide to Using the Calculator
Follow these steps to calculate the area under a polar curve:
- Step 1: Open the Polar Curve Area Calculator.
- Step 2: Input the polar equation (e.g., r = 2 + 3sin(θ)).
- Step 3: Set the lower and upper limits of integration (e.g., 0 to 2π).
- Step 4: Click “Calculate” to get the area.
✨ Note: Double-check the equation and limits to avoid errors.
Checklist for Using the Polar Curve Area Calculator
- Verify the polar equation is correctly formatted.
- Ensure the limits of integration are in radians.
- Check the result against known values for validation.
- Use the tool for both simple and complex polar curves.
In summary, a Polar Curve Area Calculator is an indispensable tool for anyone working with polar coordinates. It simplifies integration, saves time, and ensures precision. Whether you’re tackling academic problems or professional projects, this calculator streamlines the process, making complex calculations manageable. (polar curve area, integration tool, mathematical efficiency)
What is the formula for calculating the area under a polar curve?
+The formula is A = (1/2) ∫[a, b] r² dθ, where r is the polar equation and θ is the angle.
Can I use the calculator for any polar equation?
+Yes, the calculator works for most polar equations, provided they are correctly formatted.
Are the limits of integration always in radians?
+Yes, the limits should be in radians for accurate results.
Is the Polar Curve Area Calculator free to use?
+Many online calculators are free, but features may vary depending on the platform.
Can I use this tool for educational purposes?
+Absolutely! It’s a great resource for students and educators to practice and teach polar integration.



