Master Central Angles & Arc Measures: Essential Geometry Tips
<!DOCTYPE html>
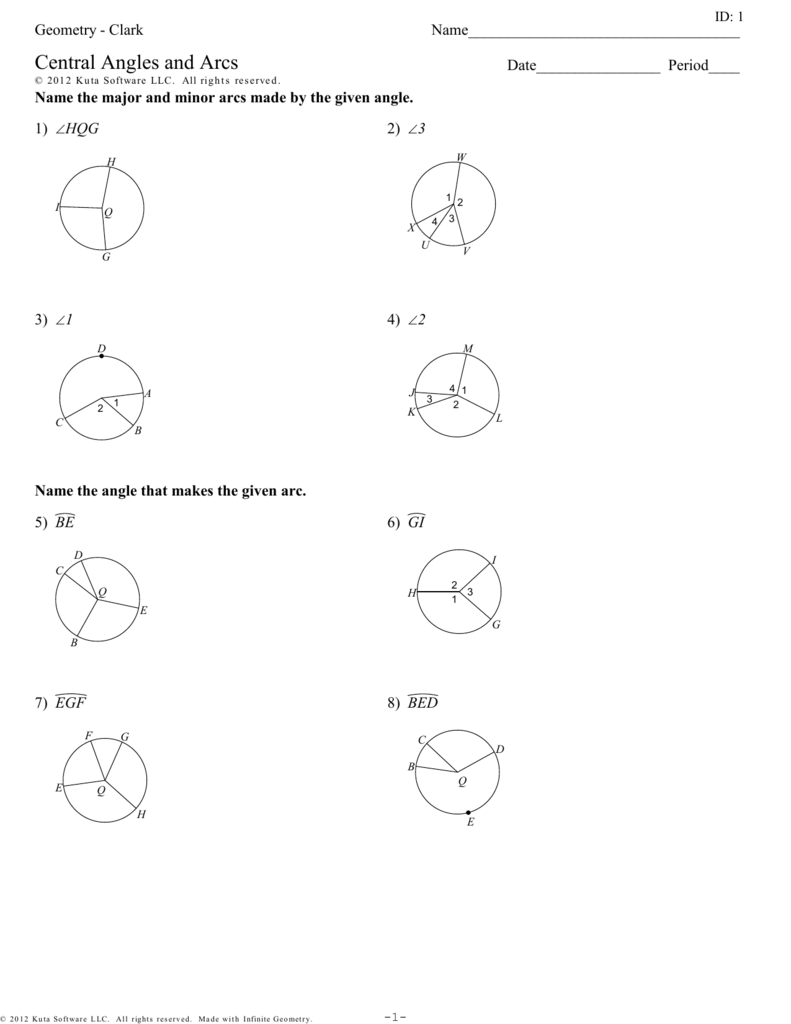
Understanding central angles and arc measures is crucial for mastering geometry. These concepts are fundamental in circles and have wide-ranging applications in mathematics, engineering, and design. Whether you’re a student preparing for exams or a professional needing a refresher, this guide will help you grasp these essential geometry topics. (geometry tips, central angles, arc measures)
What Are Central Angles and Arc Measures?

A central angle is an angle whose vertex is at the center of a circle, and its sides pass through two points on the circle’s circumference. The arc measure, on the other hand, is the length of the arc subtended by the central angle. These two concepts are interconnected and play a vital role in solving circle-related problems. (central angles, arc measures, circle geometry)
How to Calculate Central Angles and Arc Measures

Step 1: Understand the Relationship
The measure of a central angle is directly proportional to the arc length it intercepts. The formula to relate these is: Arc Length = (central angle / 360) × Circumference. This relationship is key to solving problems involving circles. (central angles, arc measures, circle formulas)
Step 2: Use Proportions for Partial Circles
When dealing with sectors or segments, use proportions to find arc measures or central angles. For example, if a central angle is 60 degrees, the arc length is (60⁄360) × Circumference. This method simplifies calculations for partial circle areas. (arc measures, central angles, circle sectors)
📘 Note: Always ensure the angle is in degrees when using the 360-degree denominator.
Practical Applications of Central Angles and Arc Measures
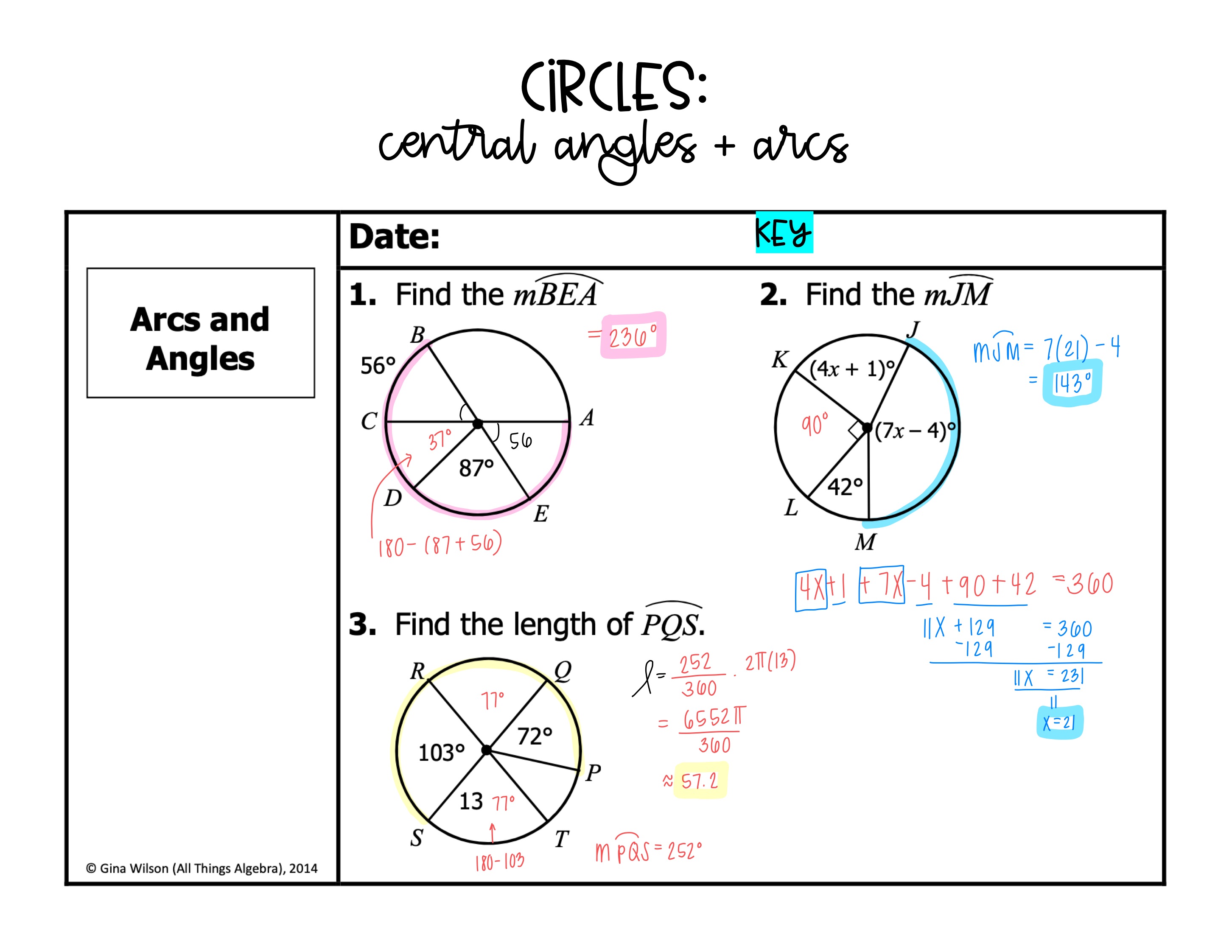
These concepts are not just theoretical; they have real-world applications. For instance, architects use them to design curved structures, and engineers apply them in calculating wheel rotations. Understanding these principles enhances problem-solving skills across various fields. (geometry applications, central angles, arc measures)
Checklist for Mastering Central Angles and Arc Measures
- Understand the definition of central angles and arc measures.
- Learn the formula relating central angles to arc lengths.
- Practice solving problems involving sectors and segments.
- Apply these concepts to real-world scenarios.
By following these steps and practicing regularly, you’ll gain confidence in handling central angles and arc measures. These skills are not only essential for geometry but also lay the foundation for advanced mathematical concepts. (geometry mastery, central angles, arc measures)
What is a central angle?
+A central angle is an angle whose vertex is at the center of a circle, with its sides passing through two points on the circumference.
How do you calculate arc length?
+Arc length is calculated using the formula: Arc Length = (central angle / 360) × Circumference.
Why are central angles important in geometry?
+Central angles are crucial for understanding circle properties, calculating areas, and solving real-world problems in fields like engineering and architecture.



