Mastering Compounded Interest Word Problems: Real-Life Examples

<!DOCTYPE html>
Compounded interest is a powerful financial concept that can significantly impact your savings or investments over time. Understanding how it works in real-life scenarios is crucial for making informed financial decisions. Whether you’re planning for retirement, saving for a home, or investing in the stock market, mastering compounded interest word problems will empower you to maximize your financial growth. In this blog, we’ll explore practical examples, step-by-step solutions, and essential tips to help you grasp this concept effortlessly. (compounded interest, financial planning, investment strategies)
What is Compounded Interest and Why Does It Matter?

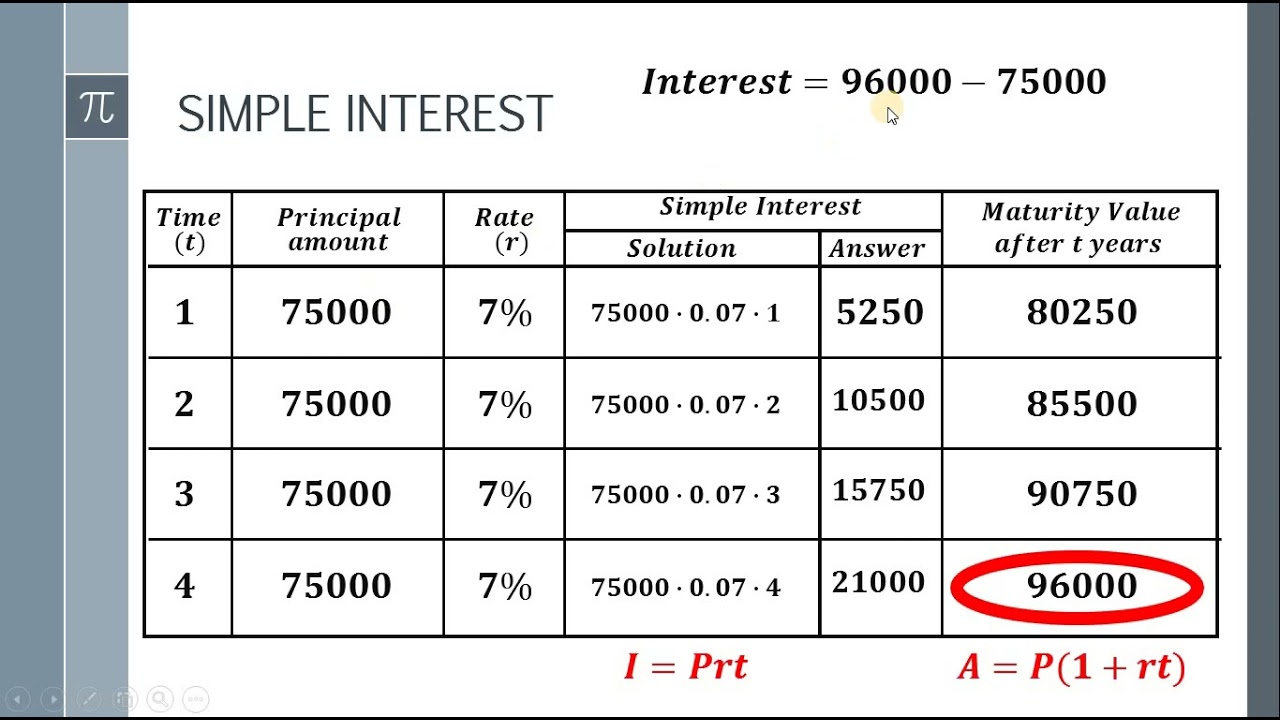
Compounded interest is the interest calculated on the initial principal and also on the accumulated interest of previous periods. Unlike simple interest, which is calculated only on the principal amount, compounded interest leads to exponential growth over time. This makes it a critical concept for long-term financial planning.
💡 Note: The frequency of compounding (e.g., annually, quarterly, monthly) affects the total amount earned or owed.
Real-Life Examples of Compounded Interest Word Problems

Example 1: Savings Account
Imagine you deposit 5,000 into a savings account with an annual interest rate of 3%, compounded annually. How much will you have after 10 years?</p> <p><strong>Solution:</strong> Using the formula A = P(1 + \frac{r}{n})^{nt} , where:</p> <ul> <li> A = the amount of money accumulated after n years, including interest.</li> <li> P = the principal amount (initial deposit).</li> <li> r = annual interest rate (decimal).</li> <li> n = number of times interest is compounded per year.</li> <li> t = time the money is invested for in years.</li> </ul> <p>Plugging in the values: A = 5000(1 + \frac{0.03}{1})^{1 \times 10} = 5000(1.03)^{10} \approx \6,719.58 ).
Example 2: Credit Card Debt
You have a credit card balance of 2,000 with an annual interest rate of 18%, compounded monthly. If you make no payments, how much will you owe after 2 years?</p> <p><strong>Solution:</strong> Using the same formula, but adjusting for monthly compounding ( n = 12 ):</p> <p> A = 2000(1 + \frac{0.18}{12})^{12 \times 2} \approx \2,833.59 ).
⚠️ Note: High-interest debt can grow rapidly due to compounding, making timely payments essential.
Tips for Solving Compounded Interest Word Problems

- Identify Key Variables: Always note the principal, interest rate, compounding frequency, and time period.
- Use the Correct Formula: The compound interest formula is your go-to tool for these problems.
- Practice Regularly: The more you practice, the better you’ll become at solving these problems quickly.
Checklist for Mastering Compounded Interest
- Understand the difference between simple and compounded interest.
- Memorize the compound interest formula and its variables.
- Practice solving real-life word problems regularly.
- Use online calculators to verify your solutions.
- Apply your knowledge to personal financial planning.
Mastering compounded interest word problems is not just about solving equations—it’s about understanding how money grows or shrinks over time. By applying these concepts to real-life scenarios, you can make smarter financial decisions and achieve your long-term goals. (financial literacy, compound interest calculator, savings growth)
What is the difference between simple and compounded interest?
+Simple interest is calculated only on the principal amount, while compounded interest is calculated on the principal and the accumulated interest from previous periods.
How often should interest be compounded for maximum growth?
+The more frequently interest is compounded (e.g., daily or monthly), the greater the growth, as interest earns interest more often.
Can compounded interest work against me?
+Yes, compounded interest can work against you in high-interest debt scenarios, such as credit cards, causing your debt to grow rapidly if not managed properly.


