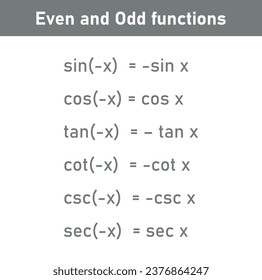
Understanding even and odd trigonometric functions is essential for mastering trigonometry. These properties simplify complex problems and enhance your problem-solving skills. Whether you're a student, educator, or enthusiast, this guide breaks down the concepts into easy-to-follow steps, ensuring clarity and confidence in your mathematical journey. (Trigonometric Identities, Even Functions, Odd Functions)
What Are Even and Odd Trigonometric Functions?
In trigonometry, functions are classified as even or odd based on their symmetry. An even function satisfies the condition ( f(-x) = f(x) ), while an odd function satisfies ( f(-x) = -f(x) ). This classification helps in simplifying equations and understanding graph behavior. (Trigonometric Functions, Even and Odd Properties)
| Function | Type | Example |
|---|---|---|
| \cos(x) | Even | \cos(-x) = \cos(x) |
| \sin(x) | Odd | \sin(-x) = -\sin(x) |
How to Identify Even and Odd Functions
Identifying whether a trigonometric function is even or odd involves checking its symmetry. Here’s a step-by-step approach:
- Step 1: Substitute (-x) into the function.
- Step 2: Simplify the expression.
- Step 3: Compare the result with the original function.
📌 Note: Always ensure the function is defined for both (x) and (-x).
Practical Applications of Even and Odd Functions
Mastering these properties has real-world applications, such as in physics, engineering, and computer graphics. For instance, even functions are used in modeling symmetric phenomena, while odd functions represent antisymmetric behaviors. (Applications of Trigonometry, Mathematical Modeling)
Checklist: Mastering Even and Odd Trigonometric Functions
- Understand the definitions of even and odd functions.
- Practice identifying even and odd trigonometric functions.
- Apply these properties to simplify trigonometric expressions.
- Explore real-world applications to reinforce learning.
By mastering even and odd trigonometric functions, you’ll gain a deeper understanding of trigonometry and its applications. Use this guide as a foundation to tackle more advanced topics with confidence. (Trigonometry Basics, Mathematical Concepts)
What is an even trigonometric function?
+
An even trigonometric function satisfies ( f(-x) = f(x) ). Examples include ( \cos(x) ). (Even Functions)
What is an odd trigonometric function?
+
An odd trigonometric function satisfies ( f(-x) = -f(x) ). Examples include ( \sin(x) ). (Odd Functions)
Why are even and odd functions important in trigonometry?
+
They simplify equations, help in graphing, and are essential in various mathematical and scientific applications. (Trigonometric Simplification)
