Understanding Hooke's Law: The Role of the K Constant

Hooke's Law is a fundamental principle in physics that describes the behavior of springs and elastic materials under stress. Central to this law is the spring constant (k), a value that determines how much a spring will stretch or compress under a given force. Understanding the role of the k constant is essential for engineers, physicists, and anyone working with materials that exhibit elastic properties. Whether you're designing mechanical systems or analyzing material behavior, grasping this concept is crucial. (Hooke's Law, spring constant, elastic materials)
What is Hooke’s Law?

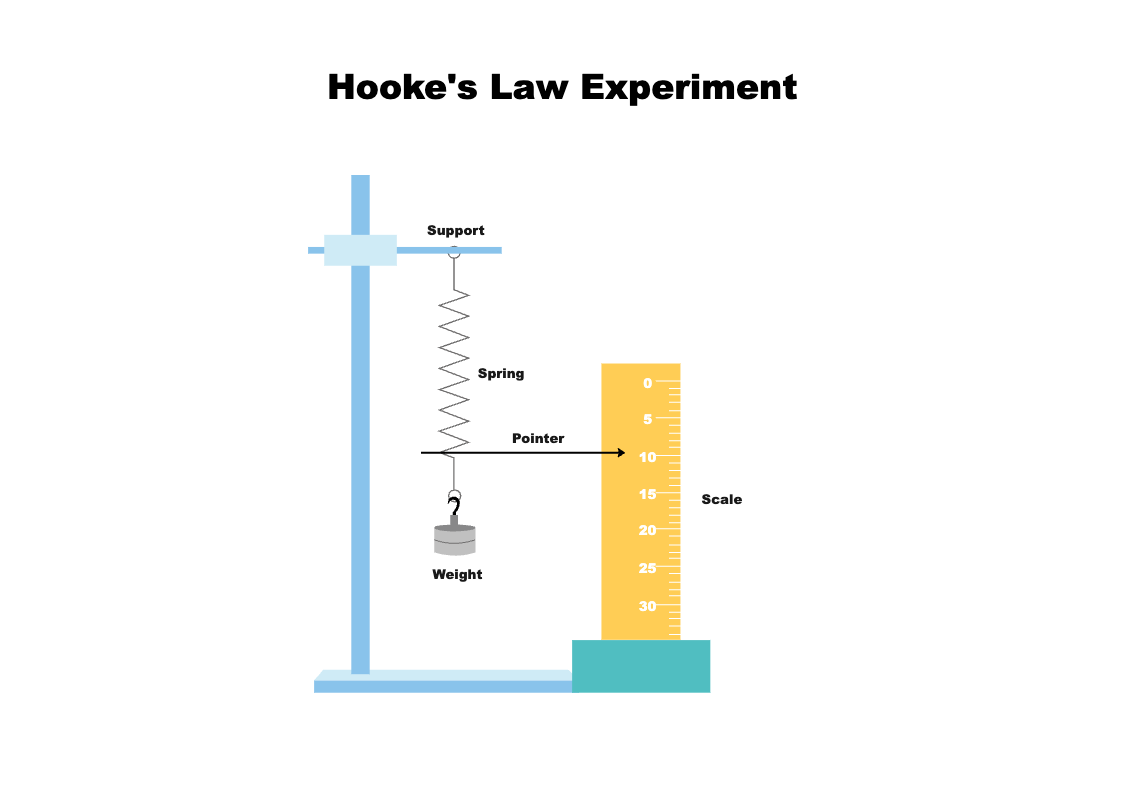
Hooke’s Law states that the force (F) required to extend or compress a spring is directly proportional to the distance (x) it is stretched or compressed, provided the material does not exceed its elastic limit. Mathematically, it is expressed as:
F = -kx,
where:
- F is the force applied,
- k is the spring constant,
- x is the displacement from the equilibrium position.
This law applies to various materials, not just springs, as long as they behave elastically. (Hooke’s Law equation, elastic limit, force and displacement)
The Role of the Spring Constant (k)

The spring constant (k) is a measure of a material’s stiffness. A higher k value indicates a stiffer material that requires more force to deform, while a lower k value suggests greater flexibility. This constant is unique to each material and remains unchanged as long as the material behaves elastically. For example, steel has a higher k than rubber, making it less deformable under the same force. (spring constant definition, material stiffness, elastic behavior)
How to Calculate the Spring Constant
To determine the spring constant (k), you can use the formula derived from Hooke’s Law:
k = F / x.
Simply measure the force applied to the spring and the resulting displacement. This calculation is vital in material testing and engineering applications. (spring constant calculation, force measurement, displacement measurement)
📌 Note: Ensure the material remains within its elastic limit to avoid permanent deformation.
Applications of Hooke’s Law
Hooke’s Law is widely applied in:
- Mechanical Engineering: Designing suspension systems and shock absorbers.
- Material Science: Testing the elasticity of polymers and metals.
- Automotive Industry: Developing springs for vehicles.
Understanding the k constant ensures optimal performance and safety in these applications. (mechanical engineering, material science, automotive applications)
| Material | Spring Constant (k) [N/m] |
|---|---|
| Steel | 200,000 - 500,000 |
| Rubber | 100 - 1,000 |
| Copper | 120,000 - 150,000 |
Factors Affecting the Spring Constant

The spring constant (k) depends on:
- Material Properties: Young’s modulus and shear modulus.
- Geometry: Shape and dimensions of the spring.
- Temperature: Can alter material stiffness.
These factors must be considered when selecting materials for specific applications. (material properties, spring geometry, temperature effects)
- Ensure the material operates within its elastic limit.
- Measure force and displacement accurately for k calculation.
- Account for material properties and geometry in design.
- Test materials under controlled conditions to determine k.
In summary, Hooke's Law and the spring constant (k) are fundamental concepts in understanding elastic behavior. By mastering these principles, you can effectively analyze materials, design systems, and ensure optimal performance in various applications. Whether you're in engineering, physics, or material science, this knowledge is indispensable. (Hooke's Law summary, spring constant importance, elastic behavior analysis)
What is Hooke’s Law?
+
Hooke’s Law states that the force applied to a spring is directly proportional to its displacement, given by the equation F = -kx.
How is the spring constant (k) calculated?
+
The spring constant (k) is calculated using the formula k = F / x, where F is the force and x is the displacement.
What factors affect the spring constant?
+
The spring constant is affected by material properties, geometry, and temperature.