Ratio Test for Series Convergence Explained

Understanding the Ratio Test for Series Convergence is crucial for anyone studying calculus or advanced mathematics. This test helps determine whether an infinite series converges or diverges by analyzing the behavior of its terms. Whether you’re a student, educator, or math enthusiast, mastering this concept will enhance your problem-solving skills and deepen your understanding of series.
What is the Ratio Test?
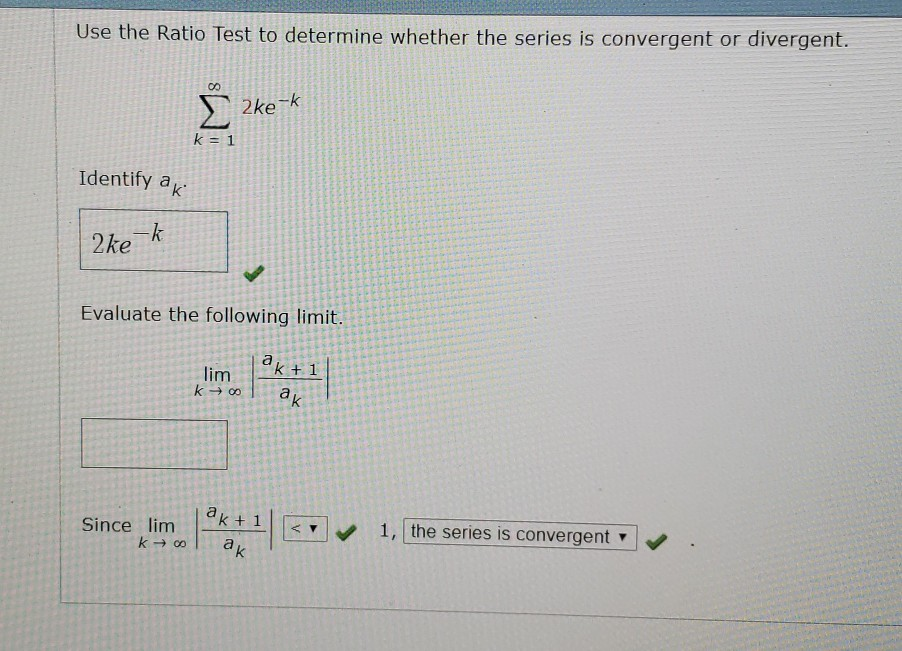
The Ratio Test is a method used to determine the convergence or divergence of an infinite series. It involves comparing the ratio of consecutive terms in the series to a limit. If this limit is less than 1, the series converges; if it’s greater than 1, the series diverges; and if it equals 1, the test is inconclusive.
How Does the Ratio Test Work?
For a series ∑aₙ, the Ratio Test examines the limit of |aₙ₊₁ / aₙ| as n approaches infinity. Here’s a step-by-step breakdown:
1. Identify the Terms: Write down the general term aₙ of the series.
2. Form the Ratio: Compute the ratio |aₙ₊₁ / aₙ|.
3. Evaluate the Limit: Find the limit of this ratio as n approaches infinity.
4. Apply the Rule:
- If the limit is less than 1, the series converges.
- If the limit is greater than 1, the series diverges.
- If the limit is equal to 1, the test is inconclusive.
📌 Note: The Ratio Test is particularly useful for series involving factorials, exponentials, or powers of n.
When to Use the Ratio Test

The Ratio Test is most effective for series where the terms involve expressions that become simpler when divided by each other. Examples include:
- Series with factorials (e.g., n! or (2n)!).
- Series with exponential terms (e.g., eⁿ or 2ⁿ).
- Series with powers of n (e.g., nᵏ or 1/nᵏ).
Example Application
Consider the series ∑(n! / nⁿ). Using the Ratio Test:
1. Form the ratio: |(n+1)! / (n+1)ⁿ⁺¹| / |n! / nⁿ|.
2. Simplify the ratio: [(n+1)! / n!] * [nⁿ / (n+1)ⁿ⁺¹].
3. Evaluate the limit as n → ∞.
| Step | Calculation | Result |
|---|---|---|
| Ratio | (n+1) * (n/n+1)ⁿ | Limit = 0 (converges) |

Key Takeaways

- The Ratio Test is a powerful tool for determining series convergence.
- It works best for series with terms involving factorials, exponentials, or powers.
- The test is inconclusive if the limit equals 1.
To summarize, the Ratio Test simplifies the analysis of complex series by focusing on the behavior of consecutive terms. By mastering this technique, you’ll gain confidence in tackling advanced calculus problems.
What is the Ratio Test used for?
+The Ratio Test is used to determine whether an infinite series converges or diverges by analyzing the limit of the ratio of consecutive terms.
When is the Ratio Test inconclusive?
+The Ratio Test is inconclusive when the limit of the ratio of consecutive terms equals 1.
Can the Ratio Test be applied to all series?
+No, the Ratio Test works best for series with terms involving factorials, exponentials, or powers. Other tests may be more suitable for different types of series.
series convergence,ratio test examples,calculus tutorials,infinite series analysis