Rotational Inertia of a Rod: Simplified Explained Guide
Understanding the rotational inertia of a rod is crucial for anyone studying physics or engineering. Rotational inertia, also known as the moment of inertia, measures an object’s resistance to changes in its rotational motion. For a rod, this concept becomes particularly interesting due to its shape and mass distribution. Whether you’re a student, a hobbyist, or a professional, this guide simplifies the topic, making it accessible and actionable. (rotational inertia, moment of inertia, physics concepts)
What is Rotational Inertia?
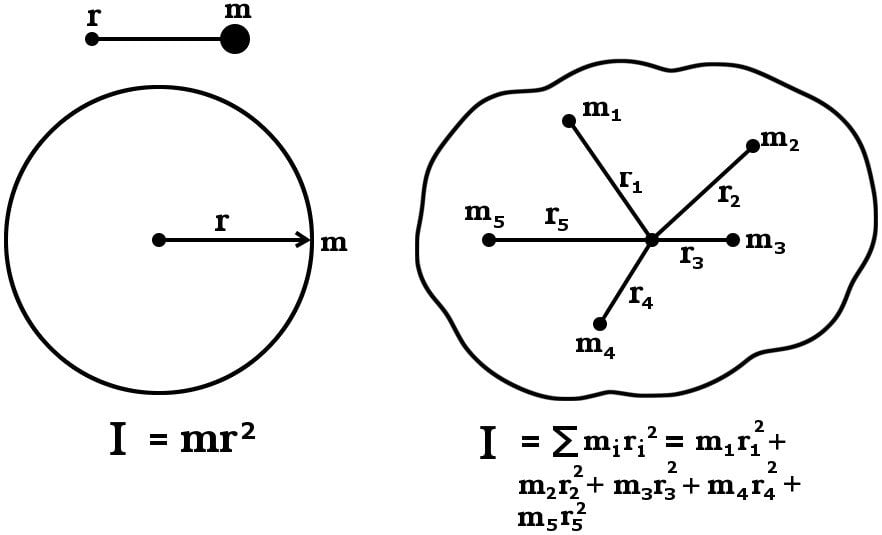
Rotational inertia quantifies how difficult it is to start or stop an object’s rotation. It depends on two factors: the mass of the object and its distribution relative to the axis of rotation. For a rod, the formula varies based on whether it rotates about its center or one of its ends. (rotational inertia definition, moment of inertia formula)
Formula for Rotational Inertia of a Rod

The rotational inertia of a rod depends on its orientation. Here are the key formulas:
- Rotation about the center: ( I = \frac{1}{12}ML^2 )
- Rotation about one end: ( I = \frac{1}{3}ML^2 )
Where:
- ( M ) = mass of the rod
- ( L ) = length of the rod
These formulas highlight how the axis of rotation affects the moment of inertia. (rotational inertia formula, moment of inertia of a rod)
| Axis of Rotation | Formula |
|---|---|
| Center | \frac{1}{12}ML^2 |
| End | \frac{1}{3}ML^2 |

💡 Note: Always ensure the units for mass (kg) and length (m) are consistent for accurate calculations.
Why Does Rotational Inertia Matter?

Understanding rotational inertia is essential in various applications, from designing machinery to analyzing sports equipment. For example, a baseball bat’s rotational inertia affects how easily a player can swing it. (practical applications, rotational inertia in engineering)
How to Calculate Rotational Inertia Step-by-Step

- Identify the axis of rotation: Determine if the rod rotates about its center or one end.
- Measure the mass (M): Use a scale to find the rod’s mass.
- Measure the length (L): Use a measuring tape to determine the rod’s length.
- Apply the formula: Use the appropriate formula based on the axis of rotation.
- Calculate: Plug in the values and solve for ( I ).
📝 Note: Double-check your measurements to avoid errors in calculations.
Practical Tips for Applying Rotational Inertia

- Engineering: Use rotational inertia to design balanced rotating systems.
- Physics Experiments: Verify theoretical calculations with practical experiments.
- Sports: Optimize equipment performance by understanding its rotational inertia.
Checklist for Mastering Rotational Inertia
- [ ] Understand the definition of rotational inertia.
- [ ] Memorize the formulas for a rod’s moment of inertia.
- [ ] Practice calculating ( I ) for different scenarios.
- [ ] Apply the concept to real-world problems.
To summarize, the rotational inertia of a rod is a fundamental physics concept with wide-ranging applications. By mastering the formulas and understanding their implications, you can tackle complex problems with confidence. Whether you’re studying for an exam or working on a project, this guide provides the clarity you need. (rotational inertia, moment of inertia, physics applications)
What is rotational inertia?
+
Rotational inertia, or moment of inertia, measures an object’s resistance to changes in its rotational motion.
How does the axis of rotation affect a rod’s inertia?
+
The moment of inertia increases when the rod rotates about its end compared to its center.
Why is rotational inertia important in engineering?
+
It helps design balanced systems, ensuring efficiency and safety in rotating machinery.



