Understanding the SAS Fisher Exact Test: A Quick Guide
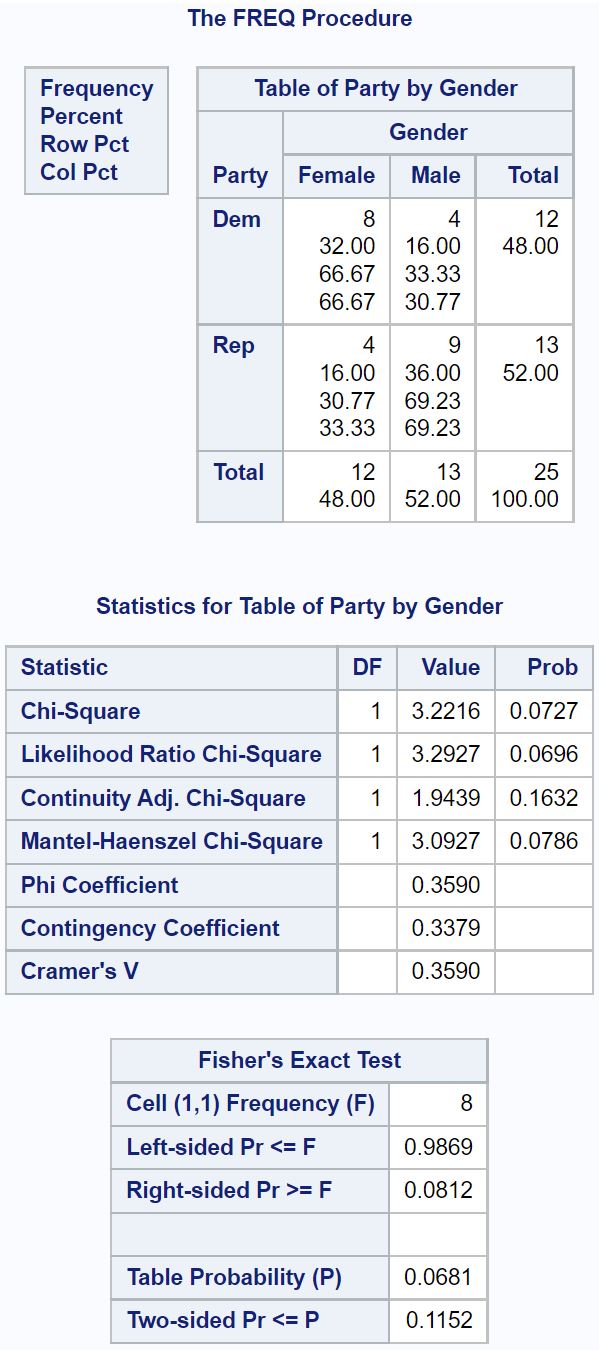
The SAS Fisher Exact Test is a powerful statistical tool used to analyze the association between two categorical variables, particularly when dealing with small sample sizes. Unlike the Chi-Square test, which relies on asymptotic assumptions, the Fisher Exact Test provides exact probabilities, making it a more reliable choice in certain scenarios. Whether you're a data analyst, researcher, or statistician, understanding this test can significantly enhance your data analysis capabilities. (SAS Fisher Exact Test, Statistical Analysis, Data Analysis)
What is the SAS Fisher Exact Test?

The SAS Fisher Exact Test is a non-parametric statistical test used to determine if there is a significant association between two categorical variables. It is particularly useful when the sample size is small, and the assumptions of the Chi-Square test are not met. The test calculates the exact probability of obtaining the observed data, given the marginal totals, without relying on asymptotic approximations. (Fisher Exact Test, Non-Parametric Test, Chi-Square Test)
When to Use the SAS Fisher Exact Test

The SAS Fisher Exact Test is ideal in the following situations:
- Small Sample Sizes: When the sample size is small, the Chi-Square test may not be accurate.
- Sparse Data: When the expected frequencies in one or more cells of the contingency table are less than 5.
- Exact Probabilities Needed: When you require exact p-values rather than approximations.
📊 Note: Always consider the nature of your data and sample size before choosing between the Fisher Exact Test and the Chi-Square test. (Small Sample Sizes, Sparse Data, Exact Probabilities)
How to Perform the SAS Fisher Exact Test

Performing the SAS Fisher Exact Test involves the following steps:
- Prepare Your Data: Organize your data into a contingency table with rows and columns representing the categories of your variables.
- Use the FREQ Procedure: In SAS, the FREQ procedure is used to perform the Fisher Exact Test. Specify the tables and the exact option.
- Interpret the Results: Examine the p-value to determine if there is a significant association between the variables.
💻 Note: Ensure your data is correctly formatted before running the test to avoid errors. (FREQ Procedure, Contingency Table, P-Value)
Example of SAS Fisher Exact Test

Consider a study examining the relationship between smoking and lung cancer. The data is organized into a 2x2 contingency table:
| Lung Cancer | No Lung Cancer | |
|---|---|---|
| Smoker | 30 | 20 |
| Non-Smoker | 10 | 40 |

Using the FREQ procedure in SAS, you can calculate the exact p-value to determine if smoking is significantly associated with lung cancer. (Contingency Table, FREQ Procedure, P-Value)
Summary Checklist

- Understand when to use the SAS Fisher Exact Test.
- Prepare your data in a contingency table.
- Use the FREQ procedure in SAS with the exact option.
- Interpret the p-value to draw conclusions.
The SAS Fisher Exact Test is an essential tool for analyzing associations between categorical variables, especially in small datasets. By following the steps outlined in this guide, you can effectively perform and interpret the test in SAS. Whether you're conducting research or analyzing data, mastering this test will enhance your statistical toolkit. (SAS Fisher Exact Test, Statistical Analysis, Data Analysis)
What is the difference between the Fisher Exact Test and the Chi-Square test?
+The Fisher Exact Test provides exact probabilities and is suitable for small sample sizes, while the Chi-Square test relies on asymptotic assumptions and is better for larger datasets. (Fisher Exact Test, Chi-Square Test)
Can the Fisher Exact Test handle more than 2x2 tables?
+Yes, the Fisher Exact Test can be extended to larger tables, but computations become more complex and time-consuming. (Contingency Table, Fisher Exact Test)
How do I interpret the p-value from the Fisher Exact Test?
+A p-value less than your significance level (commonly 0.05) indicates a significant association between the variables. (P-Value, Significance Level)



