Solving Triangles: Sine Rule Ambiguous Case Explained

Solving triangles is a fundamental skill in trigonometry, but it’s not always straightforward. One of the trickiest aspects is dealing with the Sine Rule Ambiguous Case, which occurs when you have two sides and an angle opposite one of them (SSA). This scenario can lead to zero, one, or two solutions, making it essential to understand the conditions and steps to solve it accurately. Whether you’re a student, educator, or professional, mastering this concept will enhance your problem-solving abilities in geometry and trigonometry.
Understanding the Sine Rule Ambiguous Case

The Sine Rule states that in any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. Mathematically, it’s expressed as:
a/sin(A) = b/sin(B) = c/sin©.
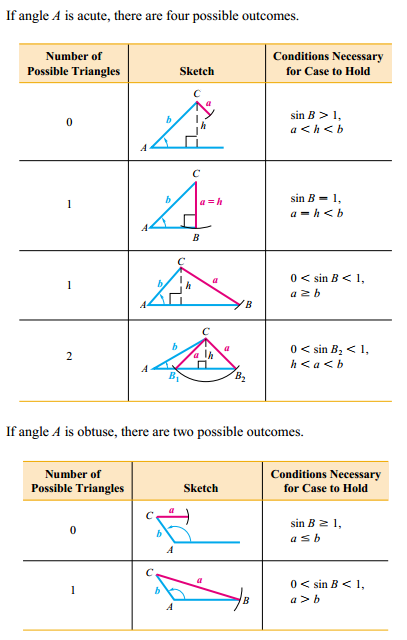
However, when given two sides and an angle opposite one of them (SSA), the problem becomes ambiguous. This is because the given angle can correspond to one, two, or no triangles depending on the relationship between the sides and the angle.
Why is the SSA Case Ambiguous?
In the SSA case, the position of the given angle relative to the sides determines the number of possible solutions. Here’s a breakdown:
- One Solution: When the given side opposite the angle is shorter than the other side.
- Two Solutions: When the given side is longer than the other side but shorter than the sum of the other side and the angle’s opposite side.
- No Solution: When the given side is too long to form a triangle with the other side and the angle.
📌 Note: Always check the relationship between the sides and the angle before solving to avoid errors.
Steps to Solve the Ambiguous Case

To tackle the Sine Rule Ambiguous Case, follow these systematic steps:
Step 1: Identify the Given Information
Clearly label the sides and angles provided in the problem. Ensure you have two sides and an angle opposite one of them (SSA).
Step 2: Apply the Sine Rule
Use the Sine Rule to find the possible measure of the second angle. The formula is:
sin(B) = (b * sin(A)) / a.
Step 3: Determine the Number of Solutions
Based on the relationship between the sides and the angle, decide whether there are zero, one, or two possible triangles.
Step 4: Solve for the Remaining Angles and Sides
If there is one or two solutions, use the Sine Rule or Cosine Rule to find the remaining angles and sides.
📌 Note: Always verify your solutions by checking if they satisfy the triangle inequality theorem.
Checklist for Solving the Ambiguous Case

To ensure accuracy, follow this checklist:
- Identify the SSA configuration in the problem.
- Apply the Sine Rule to find the possible second angle.
- Check the relationship between the sides and the angle to determine the number of solutions.
- Use additional rules (like the Cosine Rule) to solve for remaining elements.
- Verify all solutions to ensure they form valid triangles.
Practical Example of the Ambiguous Case

Consider a triangle with sides a = 5, b = 7, and angle A = 30°. Let’s solve it step-by-step:
1. Apply the Sine Rule: sin(B) = (7 * sin(30°)) / 5.
2. Calculate sin(B): sin(B) = (7 * 0.5) / 5 = 0.7.
3. Find angle B: B = sin⁻¹(0.7) ≈ 44.43° or B = 180° - 44.43° = 135.57°.
4. Determine the number of solutions: Since a < b, there are two possible triangles.
| Case | Angle B | Possible Triangle |
|---|---|---|
| 1 | 44.43° | Valid |
| 2 | 135.57° | Valid |

Wrapping Up
The Sine Rule Ambiguous Case is a challenging but manageable concept in trigonometry. By understanding the conditions for zero, one, or two solutions and following a systematic approach, you can solve SSA problems with confidence. Remember to always verify your solutions and use additional rules when necessary.
What is the Sine Rule Ambiguous Case?
+The Sine Rule Ambiguous Case occurs when solving triangles with two sides and an angle opposite one of them (SSA), leading to zero, one, or two possible solutions.
How do I determine the number of solutions in the SSA case?
+Check the relationship between the sides and the angle. If the given side is shorter than the other side, there’s one solution. If it’s longer but not too long, there are two solutions. If it’s too long, there’s no solution.
Can the Sine Rule Ambiguous Case have no solution?
+Yes, if the given side is too long to form a triangle with the other side and the angle, there is no solution.
trigonometry,solving triangles,Sine Rule,SSA case,geometry,mathematics,


